Embedded programming, microcontrollers and FPGAs have always been incredibly appealing to me. Why? Probably because they emphasize things about development and design that I personally believe to be very important - keeping things short, efficient and simple.

Recently, I needed to draw circles with as little code as possible which always get me into the “is there a better way” mode. The traditional approach would be simply to use the

equation and if the squared coordinates sum up to the squared radius, the point lies on the circle. Yet, to calculate y from an arbitrary x, you need multiplication and square roots - things not exactly trivial in the world of simple tiny chips.

Minsky’s Circle Algorithm

There is a cool solution to this problem called the Minsky’s circle algorithm. The algorithm was stumbled upon in 1960s and is incredibly simple.

Original idea was using the old value of x to draw a spiral shape, but the programmer made a mistake and used the new value of x - the output was, mysteriously, a circle. If you use the new value of x, then the expression becomes

It resembles a rotation matrix

because for small angles cos is close to 1 and sin is close to 0:

Since its determinant is equal to 1, there is no scaling and the curve ends up being closed after a number of iterations. Instead of multiplying by an arbitrary, small number ε, we multiply by a negative power of two which is essentially equal as dividing by a power of two. This is approximated using right shifts (2^-4 is chosen for this example). The expression now becomes really simple:

Bit shifts are very efficient, and in ASIC/FPGA world they can even be free (if implemented through wire routing). This provides a good result, but not entirely accurate. Is there a way that’s just as simple, yet more accurate?

Improvement

A more recent approach by Neal and Pitteway (1990) substantially improved the accuracy. Minsky’s algorithms actually produces an ellipse tilted at 45 degrees that highly resembles a circle. Distance to the circle varies, so to compensate they introduce a second ellipse perpendicular to the original one, and perform half rotation against each of them.

This reduces maximal distance from the actual circle by several orders of magnitude.

Can we do even better?

Accuracy is already way better than any specifications required, but the fun is in trying to make it even better. Let’s take this idea further with something like:

Keeping two pairs of coordinates does slightly increase the memory and computational load, but sticking to bit shifts and additions retains the benefits provided by the original algorithm. If a large radius (2^32) is used and ε set to 2^-12, max distance from a true circle in this particular case is < 14, which is only a few nanometers to a meter. Still not exact, but accurate enough for most practical applications one could think of.

This also provides accurate trig functions - simply put the decimal point before the MSB bit and treat the rest as sin (y) and cos (x) values. Handy!

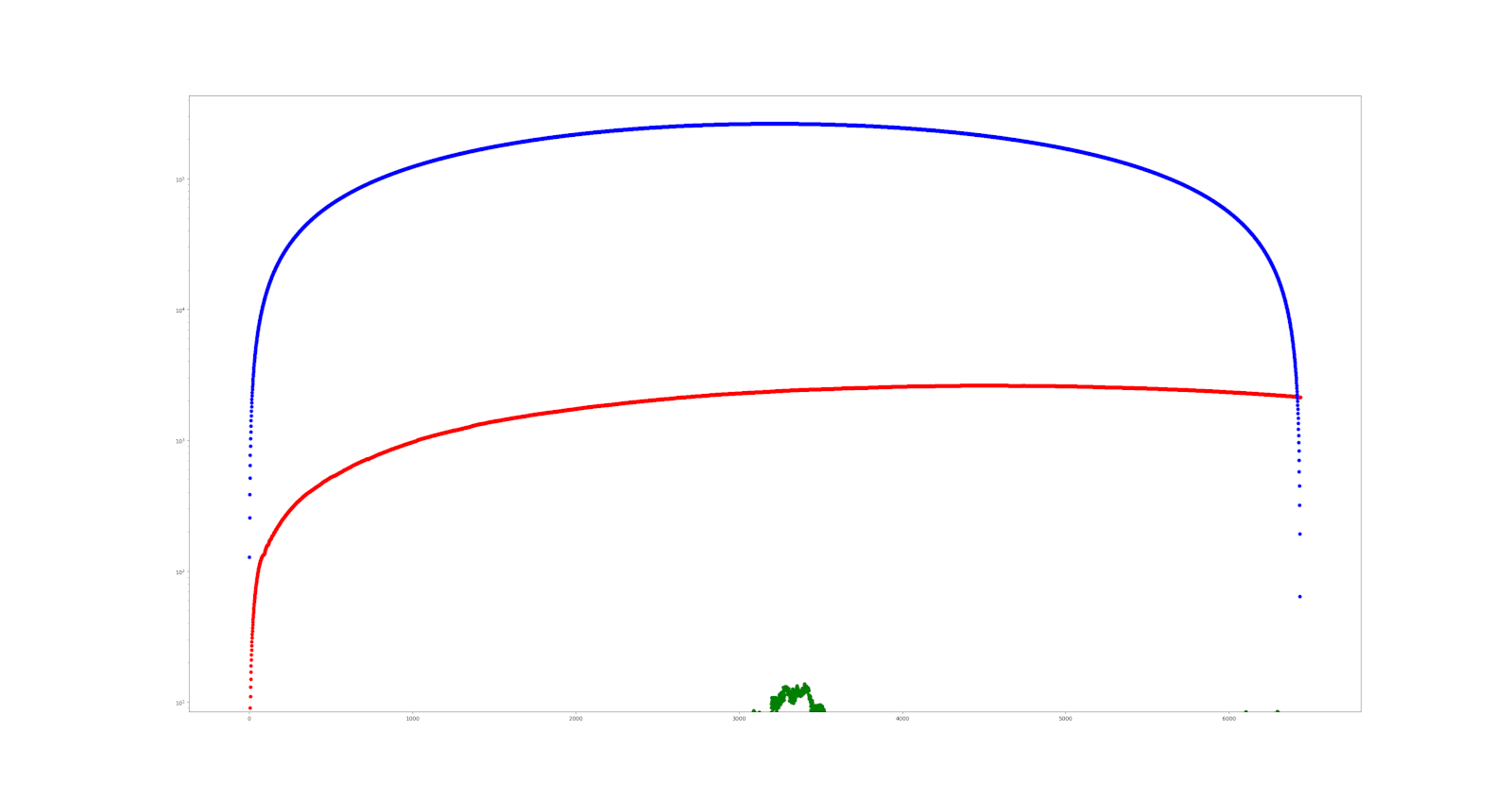
Comparison

Errors - the distances from the exact circle for the three methods are plotted and log scale is used to compensate for them being very far apart. Original method (blue) caps around 10^6, second one (red) around 10^3 and the third (green) around 10^1. And who said math isn’t amazing, fun and useful?

The year was 1984. Apple Macintosh was just introduced, as well as our own shiny new computer called “Orao” (Eagle). It ended up being chosen as a standard primary school computer in Croatia from 1985 to 1991. For many of us, kids back then, this was one of the first opportunities to ever use a computer. Simple and rudimentary by today’s standards, Orao was brilliantly designed to avoid using specialized components - only simple TTL logic and off-the-shelf parts were used.

I wanted to write a cross-platform emulator, and after making one in Python, decided to go a step further and port it to Javascript. This is perhaps the most convenient way to use it, even though not all features were ported. To invoke BASIC, enter “BC” after booting. It can fetch one of the available tape images as .wav files via AJAX and load them. Loading takes time, computers were slow back then. :-)

For a slightly more complete version, check the Python version, but if you just want a quick dose of nostalgia - HERE it is!

TL;DR: enter BC at the * (star) prompt, press ENTER when asked about the memory size and try one of the following:

LMEM "SPACEINV"
LMEM "CRVIC"
LMEM "MUZIKA"
LMEM "DEMO2"
LMEM "RUSENJE"
LMEM "TETRIS" (start with LNK4096)

Double quotes = shift + 2. To erase something, use ctrl + H or left arrow.

Lately I’ve been solving some problems on CheckiO, a really addictive programming site, and stumbled upon a very interesting golf mission. So, you might ask: “What are golf missions?!”. The idea is to solve the problem using as little code as theoretically possible. Your score is inversely related to code length and transforms a mildly challenging problem into a very addictive one.

One of the most interesting missions is called Ghost Detect. It might not seem special at first, but it gets tricky as solutions get shorter. The mission goal is to write the shortest possible code to recognize if three consecutive signals sent in binary are of the same length. 11000001100011 is a good signal while 111000100011 is a bad one. There is at least one zero between every group of ones. For each character used (less than 200) you earn 1 point. So, how do we do this?

1. Use regex (77 characters, 123 points)

import re
recognize=lambda t:len(re.findall(r'^0b(1+)0+\1{1}0+\1{1}$',bin(t)))

We find and group zeros at the beginning, followed by at least one zero, and then find exactly one occurence of the first group, then some more zeros etc. Not too complicated, but only 123 points. Can we do better?

2. Use the sets, Luke (63 characters, 137 points)

import re
recognize=lambda w:len(set(re.findall('1+',bin(w))))<2

Here we combine regex and sets to check how many different groups of repeating ones are present in binary representation.

3. Ditch the regex (57 characters, 143 points)

recognize=lambda x:len(set(bin(x)[2:].split('0'))-{''})<2

This is about as far as a “Pythonic” road will take you. Split on zeros, convert to sets, remove empty set to avoid messing with the count and check if less than two.

Now what?

To further shorten it, we need to try a different approach - binary. In binary, when you multiply by 2, you shift all the bits one position to the left. So, for example, 00010 multiplied by 2 becomes 00100. A valid signal, according to the task, is a number with three groups of ones equally long with zeros inbetween. This actually means it’s made of a number multiplied by a power of two, then the same number was multiplied by some other power of two and added, and then the same number was added again. For example, 111000111000111 is actually

Therefore, we can write a generalized form for such a number n being equal to

The number should, then, be divisible by both k and r without reminder. First variant that comes to mind is to test if n divided by k equals r. But we have neither k nor r, and the only thing we have to work with is the number given to our function. We have to think of a way to get the number using bit manipulation.

n       = 111000111000111
n+1     = 111000111001000
------------------------- XOR
n^n+1   = 000000000001111
n       = 111000111000111 
------------------------- AND
n&n^n+1 = 000000000000111

So, now we have k with some bit tricks expressed like n AND n XOR n+1. To find r, we divide n by k and realize it’s basically the original number with sequences of ones reduced to a single 1. We can achieve this too with a little bit manipulation.

n       =  111000111000111
n*2     = 1110001110001110
-------------------------- AND
n&n*2   =  110000110000110
n       =  111000111000111
-------------------------- XOR
2*n&n^n =    1000001000001

4. Bit banging:

We are testing for this simple expression.

recognize=lambda n:n/(n&n^n+1)==2*n&n^n

Down to 39 characters and 161 points. Can we do even better? Suprisingly, yes!

5. Getting rid of k

recognize=lambda n:n%(2*n&n^n)==0

If we test divisibility by k, it is easy to construct a number divisible by k which doesn’t satisfy the constraint - e.g. 110011110011. Therefore, we must test divisibility by the other factor, r. Since zeros between the ones are ensured by initial conditions, divisibility by r guarantees the required form.

Our solution is now only 33 characters long (function definition takes 19), and we scored 167 points. There is a trick to get 2 more points which I’m not going to disclose. Can you find it?

Can we go above 169?

I don’t think so, but please tell me if you think of a way! :) Hopefully you enjoyed reading about it as much as I’ve enjoyed solving it! If you have another, original solution to this problem feel free to email me and help my curiosity!

Cheers.