Embedded programming, microcontrollers and FPGAs have always been incredibly appealing to me. Why? Probably because they emphasize things about development and design that I personally believe to be very important - keeping things short, efficient and simple.

Recently, I needed to draw circles with as little code as possible which always get me into the “is there a better way” mode. The traditional approach would be simply to use the

equation and if the squared coordinates sum up to the squared radius, the point lies on the circle. Yet, to calculate y from an arbitrary x, you need multiplication and square roots - things not exactly trivial in the world of simple tiny chips.

Minsky’s Circle Algorithm

There is a cool solution to this problem called the Minsky’s circle algorithm. The algorithm was stumbled upon in 1960s and is incredibly simple.

Original idea was using the old value of x to draw a spiral shape, but the programmer made a mistake and used the new value of x - the output was, mysteriously, a circle. If you use the new value of x, then the expression becomes

It resembles a rotation matrix

because for small angles cos is close to 1 and sin is close to 0:

Since its determinant is equal to 1, there is no scaling and the curve ends up being closed after a number of iterations. Instead of multiplying by an arbitrary, small number ε, we multiply by a negative power of two which is essentially equal as dividing by a power of two. This is approximated using right shifts (2^-4 is chosen for this example). The expression now becomes really simple:

Bit shifts are very efficient, and in ASIC/FPGA world they can even be free (if implemented through wire routing). This provides a good result, but not entirely accurate. Is there a way that’s just as simple, yet more accurate?

Improvement

A more recent approach by Neal and Pitteway (1990) substantially improved the accuracy. Minsky’s algorithms actually produces an ellipse tilted at 45 degrees that highly resembles a circle. Distance to the circle varies, so to compensate they introduce a second ellipse perpendicular to the original one, and perform half rotation against each of them.

This reduces maximal distance from the actual circle by several orders of magnitude.

Can we do even better?

Accuracy is already way better than any specifications required, but the fun is in trying to make it even better. Let’s take this idea further with something like:

Keeping two pairs of coordinates does slightly increase the memory and computational load, but sticking to bit shifts and additions retains the benefits provided by the original algorithm. If a large radius (2^32) is used and ε set to 2^-12, max distance from a true circle in this particular case is < 14, which is only a few nanometers to a meter. Still not exact, but accurate enough for most practical applications one could think of.

This also provides accurate trig functions - simply put the decimal point before the MSB bit and treat the rest as sin (y) and cos (x) values. Handy!

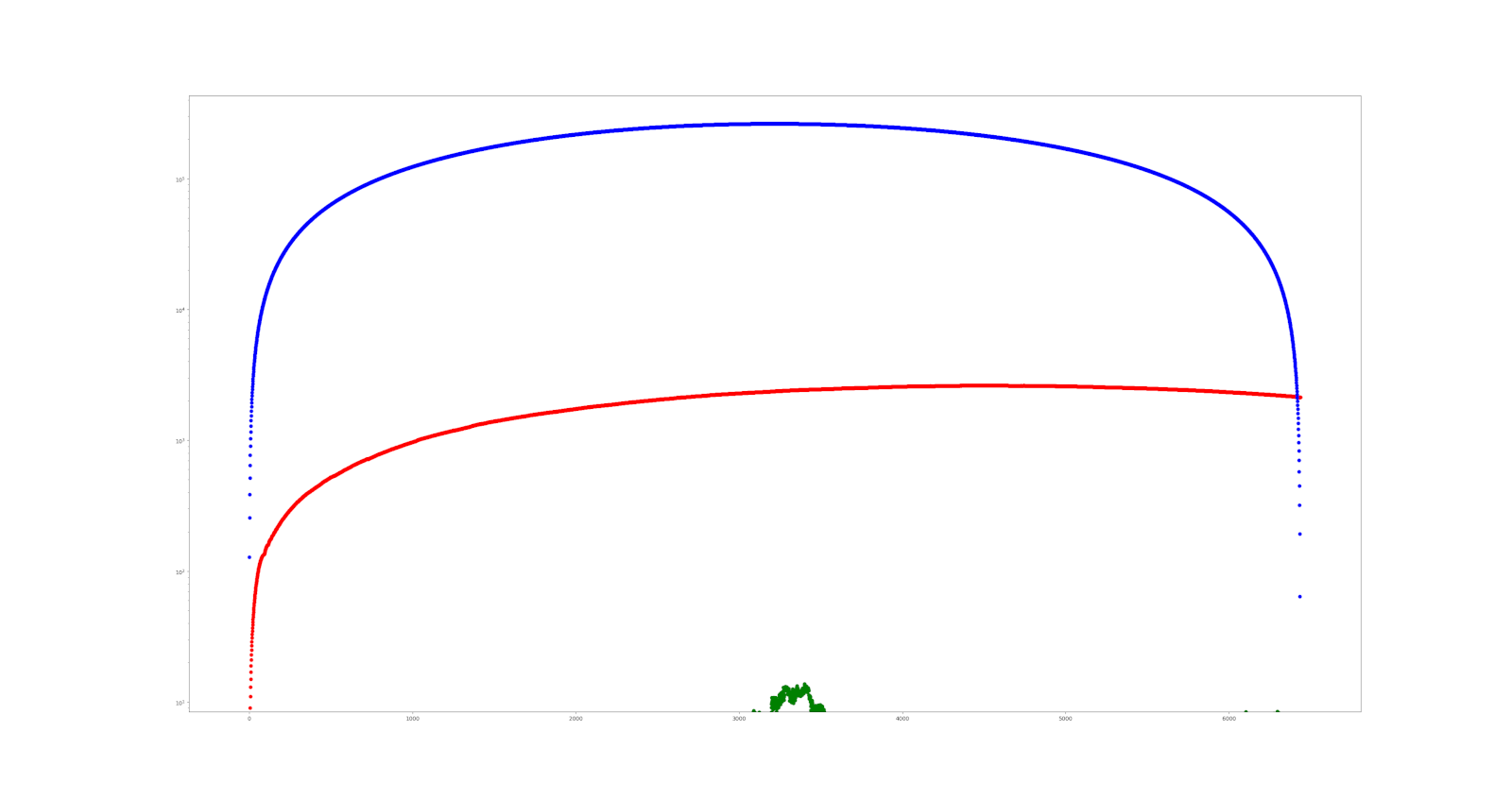
Comparison

Errors - the distances from the exact circle for the three methods are plotted and log scale is used to compensate for them being very far apart. Original method (blue) caps around 10^6, second one (red) around 10^3 and the third (green) around 10^1. And who said math isn’t amazing, fun and useful?